
Steganography OCaml
1. Introduction
This project, undertaken as part of the Algorithmics and Complexity module, involves implementing a steganography algorithm in OCaml with message encryption using the RSA algorithm.
Steganography is the practice of hiding information within an inconspicuous medium. In this project, the algorithm hides a text message within a .ppm image. This method is widely used for covert communication, as the message is virtually indistinguishable from its medium unless its existence is known.
The hidden message is also encrypted using the RSA algorithm to ensure its security. RSA is based on asymmetric encryption: a key pair is generated, consisting of a private key known only to the intended recipient for decrypting the message, and a public key used for encrypting the message, which is publicly available. This allows anyone to encrypt a message, but only the holder of the private key can decrypt it.
2. Initial Analysis
One method to discreetly encode the message into the image is by embedding the message into the least significant bits of each color channel of each pixel. This allows encoding 3 bits of data per pixel. A pixel represents 3 colors (RGB), each encoded with 8 bits, totaling 24 bits per pixel. Thus, a 100x100 pixel image can accommodate 30,000 bits of data.
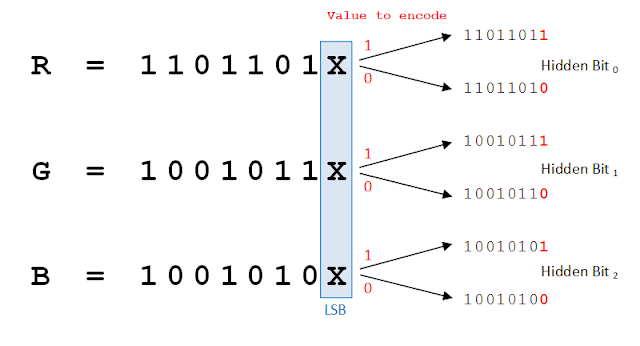 Figure 1.1: Modification of the least significant bit for each pixel.
Figure 1.1: Modification of the least significant bit for each pixel.
One initial approach for encoding the message, given its variable length, is to read the entire image: this ensures retrieval of the entire message in all cases, but the message will contain noise after its end (unaltered least significant bits). An improvement would be to write/read only up to the message length.
This is the approach chosen. A 30-bit header (10 pixels) containing the message length is implemented in the encoding/decoding section, allowing the message to be retrieved without scanning the entire image. This results in a complexity of O(n), where n is the message length.
To ensure message security, it is encrypted with RSA. The encrypted message is converted to bits before embedding to best fit the image requirements.
3. Encoding in the Image
A Portable Bitmap Format (PPM) image is a simple, uncompressed image structure containing a header with 3 lines:
- Image type indicating if the image is binary or ASCII; we use the binary type
P6. - Image width and height.
- Maximum value for each color (255 in this case).
Following the header, each pixel’s RGB values are listed.
The message length is converted to a 30-bit binary string (10 pixels). The message length is added to the first 10 pixels of the image, indicating where to stop during decoding.
3.1 Construction of the Complete Message
The message consists of the header containing the message length and the RSA-encrypted message converted to binary.
3.2 Writing into the Image
Each bit of the message is sequentially inserted into the least significant bit of each color byte of the image, overwriting the last bit with the corresponding message bit. The image is first loaded into memory, modified with the message length, and then saved as output.ppm.
3.3 Code Presentation
(* Function to overwrite the last bit of a byte with a specified bit *)
let overwrite_last_bit byte message_bit =
match message_bit with
| '1' -> byte lor 1 (* Set the last bit to 1 *)
| '0' -> byte land 0xFE (* Set the last bit to 0 *)
| _ -> failwith "Message bit must be '0' or '1'"
(* Function to insert a message into a PPM image file *)
let insert_message file_path message =
let ic = open_in_bin file_path in
let oc = open_out_bin "output.ppm" in
(* Read and rewrite the PPM header *)
let (width, height, max_val) = read_header ic in
Printf.fprintf oc "P6\n%d %d\n%s\n" width height max_val;
(* Calculate total image data size *)
let image_size = width * height * 3 in
let buffer = Bytes.create image_size in
really_input ic buffer 0 image_size; (* Load image into buffer *)
let binary_message = string_to_binary message in
let binary_length = int_to_fixed_length_binary 30 message_length in
(* Concatenate message length and the message itself *)
let full_message = binary_length ^ binary_message in
let message_index = ref 0 in
(* Iterate over each byte and insert message bits *)
for i = 0 to image_size - 1 do
if !message_index < String.length full_message then
let byte = Char.code (Bytes.get buffer i) in
let msg_bit = full_message.[!message_index] in
incr message_index; (* Move to the next message bit *)
Bytes.set buffer i (Char.chr (overwrite_last_bit byte msg_bit));
done;
(* Write the modified buffer to the output file *)
output_bytes oc buffer;
(* Close the files *)
close_in ic;
close_out oc
3.4 Complexity
Complexity of overwrite_last_bit Function
The overwrite_last_bit function modifies the last bit of a byte based on the provided bit (‘0’ or ‘1’). It uses a basic logical operation (AND or OR), executed in constant time.
- Time Complexity: O(1), as it performs a comparison and a binary operation regardless of input size.
- Space Complexity: O(1), as it uses a fixed amount of space with no additional space required based on input size.
Complexity of the Byte Processing Loop
The loop iterates over each byte of the image to insert the encoded message bits, with complexity primarily dependent on the number of bytes in the image.
- Time Complexity: O(n), where n is the total number of bytes in the image (width × height × 3). Each iteration calls
overwrite_last_bit, which runs in constant time, making the total time linear with respect to n. - Space Complexity: O(1). The loop uses a constant amount of space for variables like byte index and bit index, independent of image size or message length.
4. Message Encryption with RSA
RSA encryption is an asymmetric cryptographic system using a pair of keys: a public key for encryption and a private key for decryption. Based on the difficulty of factoring large prime numbers, RSA is widely used to secure sensitive data.
For our RSA implementation, we based it on the repository available on GitHub: RSA-by-OCaml. This repository provided a solid foundation for implementing RSA in OCaml.
4.1 Key Generation
Key generation involves the following steps:
Choose Prime Numbers: Select two large distinct prime numbers, p and q.
Calculate n: Compute . This is used in both keys.
Calculate Euler’s Totient Function :
Choose Public Exponent e:
Choose such that and . A common choice for is .Calculate Private Exponent d: is the modular inverse of modulo , meaning
4.2 Keys
Public Key: Composed of .
Private Key: Composed of .
4.3 Encryption and Decryption
- Encryption: To encrypt a message m (where m is an integer smaller than n), compute:
where c is the ciphertext.
- Decryption: To decrypt c using the private key:
where m is the original message.
4.4 Security
The security of RSA relies on the difficulty of factoring n into its prime components p and q. The size of n (typically several hundred bits) makes this task infeasible with current technology. However, proper implementation is crucial to prevent vulnerabilities, including careful selection of p, q, and e to avoid potential attacks.
4.5 Code Presentation
The RSA-related code is located in the first appendix.
Key Generation (private_key_gen)
(* Generate the private key *)
let private_key_gen rc =
let p = prime_gen rc.p_len in
let q = prime_gen rc.q_len in
let phi = Z.mul (Z.sub p Z.one) (Z.sub q Z.one) in
let e = e_gen rc phi in
let d = d_gen e phi in
{ n = Z.mul p q; p; q; e; d }
Encryption (plaintext_encrypt)
(* Encrypt plaintext using the public key *)
let plaintext_encrypt pt (pk : public_key) =
let c = Z.powm pt.message pk.e pk.n in
{ c = c; types = pt.types }
4.6 Encryption and Decryption
Encryption and decryption processes involve converting the message into an integer, performing modular exponentiation, and handling the encryption and decryption operations as described above.
4.7 Utilities and Miscellaneous Operations
- Coprimality Test (
coprime): Checks if two numbers are coprime by computing their GCD. - Serialization and File Writing: Converts data structures into string format and writes them to files for later use.
4.8 Complexity
Key Generation
- Prime Generation (
prime_gen): Uses the Miller-Rabin primality test, a probabilistic algorithm. The time complexity is dominated by modular exponentiations, denoted as O(k · log³ n), where k is the number of trials and n is the number being tested. - Private Key Generation (
private_key_gen): Involves calculating n = p × q and ϕ = (p−1)(q−1), followed by determining the private exponent d via modular inversion, with a complexity of O(log² n).
Encryption and Decryption
- Encryption (
plaintext_encrypt): Utilizes modular exponentiation with a time complexity of O(log e), where e is the public exponent, typically chosen to be small to optimize speed.
Miscellaneous Operations
- Coprimality Test (
coprime): Implements GCD calculation with logarithmic time complexity relative to the input sizes. - Serialization and File Writing: Involves I/O operations that may impact performance based on the file system used.
5. Results
Below is an example output of the program:
remybarranco@MacBook-Pro-de-Remy Projet-Algo % cat msg.txt
OCaml is the best language%
remybarranco@MacBook-Pro-de-Remy Projet-Algo % ./encode
Encrypted message inserted into the image
remybarranco@MacBook-Pro-de-Remy Projet-Algo % ./decode
Message length: 1016 bits
Decrypted Message:
OCaml is the best language
remybarranco@MacBook-Pro-de-Remy Projet-Algo %
Benchmark with 100 Iterations Each:
| Data Size | Operation | Time (seconds) |
|---|---|---|
| 10 characters (512x512 image) | Encoding | 1.520 |
| Decoding | 0.020 | |
| 100 characters (512x512 image) | Encoding | 1.360 |
| Decoding | 0.020 | |
| 10 characters (5184×3456 image) | Encoding | 1.920 |
| Decoding | 0.020 | |
| 100 characters (5184×3456 image) | Encoding | 1.820 |
| Decoding | 0.020 |
Table 1.1: Encoding and Decoding Times for Different Data Sizes
6. Conclusion
Through this report, we explored steganography and asymmetric encryption using RSA to encrypt and hide a message within an image without altering its appearance. The before and after insertion of the message into the image can be seen in Appendix 2, Figure 1.4.
Although RSA was covered in the cryptography course, we encountered it just before the project deadline. Understanding and implementing the principles of steganography was intriguing and educational. However, the syntax barrier and the learning curve of OCaml posed challenges rather than aiding in the project’s realization.
7. References
- RSA-by-OCaml
- ChatGPT
Annexes
7.1 RSA Code
(* RSA Implementation (sources/rsa.caml) *)
(* Define types for RSA configuration, public and private keys *)
type rsa_config = { p_len : int; q_len : int; e_len : int }
(* type definitions... *)
(* Function to check if two numbers are coprime *)
let coprime a b = Z.gcd a b = Z.one
(* Calculate φ(n) for a list of prime numbers (φ(n) = product of (p_i - 1)) *)
let rec prime_phi plist =
match plist with
| [] -> Z.one
| p :: plist' -> Z.mul (Z.sub p Z.one) (prime_phi plist')
(* Modular exponentiation *)
let mod_exp a b n = Z.powm a b n
(* Multiplicative modular inverse *)
let mod_minv a n = Z.invert a n
(* Generate a large random integer of specified length *)
let z_gen (len : int) =
let rec z_gen’ len acc =
if len = 0 then acc
else
z_gen’ (len - 1) (Z.add (Z.mul acc (Z.of_int 10)) (Z.of_int (Random.int 10)))
in
z_gen’ len Z.zero
(* Miller-Rabin Primality Test with configurable number of trials *)
let miller_rabin_test ?(trails = 50) n =
let rec get_factor_q num =
if Z.(mod) num (Z.of_int 2) = Z.zero then
get_factor_q (Z.div num (Z.of_int 2))
else
num
in
if Z.of_int 2 = n then true
else
let q = get_factor_q (Z.sub n Z.one) in
let rec miller_rabin_test’ trails =
if trails = 0 then true
else
let a =
Z.of_int64 (Random.int64 (Z.to_int64 (Z.min n (Z.of_int64 Int64.max_int))))
in
let rec miller_rabin_test’’ expp =
if Z.abs (Z.powm a expp n) = Z.one then miller_rabin_test’ (trails - 1)
else if expp = Z.sub n Z.one then false
else if Z.(mod) (Z.powm a expp n) n = Z.sub n Z.one then
miller_rabin_test’’ (Z.mul expp (Z.of_int 2))
else
false
in
miller_rabin_test’’ q
in
miller_rabin_test’ trails
(* Generate a prime number of a given length *)
let prime_gen ?(trails = 50) len =
let rec prime_gen’ len =
let p = z_gen len in
if miller_rabin_test ~trails p then p else prime_gen’ len
in
prime_gen’ len
(* Generate a number coprime to φ (for public exponent e) *)
let e_gen rc phi =
let rec e_gen’ phi =
let e = z_gen rc.e_len in
if coprime e phi then e else e_gen’ phi
in
e_gen’ phi
(* Generate the private exponent d using modular inverse *)
let d_gen e phi = mod_minv e phi
(* Generate a private key using RSA configuration *)
let private_key_gen rc =
let p = prime_gen rc.p_len in
let q = prime_gen rc.q_len in
let phi = Z.mul (Z.sub p Z.one) (Z.sub q Z.one) in
let e = e_gen rc phi in
let d = d_gen e phi in
{ n = Z.mul p q; p; q; e; d }
(* Generate a public key from a private key *)
let public_key_gen pk = { n = pk.n; e = pk.e }
(* Encode plaintext string to a large integer *)
let plaintext_input_string s =
let rec encode acc chars =
match chars with
| [] -> acc
| h :: t -> encode (Z.add (Z.mul acc (Z.of_int 256)) (Z.of_int (Char.code h))) t
in
let encoded = encode Z.zero (List.of_seq (String.to_seq s)) in
{ message = encoded; types = "String" }
(* Encrypt plaintext using the public key *)
let plaintext_encrypt pt (pk : public_key) =
let c = Z.powm pt.message pk.e pk.n in
{ c = c; types = pt.types }
(* Helper function to write a string to a file *)
let write_to_file ~filename ~content =
let channel = open_out filename in
output_string channel content;
close_out channel
(* Serialize a private key to a string *)
let serialize_private_key pk =
Printf.sprintf "n=%s\np=%s\nq=%s\ne=%s\nd=%s"
(Z.to_string pk.n) (Z.to_string pk.p) (Z.to_string pk.q)
(Z.to_string pk.e) (Z.to_string pk.d)
(* Serialize ciphertext to a string *)
let serialize_ciphertext c =
Z.to_string c
(* Generate and save a private key to a file *)
let private_key_gen_and_save rc filename =
let p = prime_gen rc.p_len in
let q = prime_gen rc.q_len in
let phi = Z.mul (Z.sub p Z.one) (Z.sub q Z.one) in
let e = e_gen rc phi in
let d = d_gen e phi in
let pk = { n = Z.mul p q; p; q; e; d } in
let serialized_pk = serialize_private_key pk in
write_to_file ~filename ~content:serialized_pk;
pk
(* Encrypt a message using RSA, divide into blocks, and return concatenated ciphertext *)
let encrypt_and_return_message message rc =
let pk = private_key_gen_and_save rc "private_key.txt" in
let public_key = public_key_gen pk in
let block_size = (Z.numbits pk.n) / 8 - 1 in (* Calculate block size based on key size *)
let rec encode_blocks msg acc =
if msg = "" then List.rev acc
else
let block = String.sub msg 0 (min block_size (String.length msg)) in
let remaining = String.sub msg (min block_size (String.length msg)) (String.length msg - min block_size (String.length msg)) in
let encoded = plaintext_input_string block in
let encrypted = plaintext_encrypt encoded public_key in
encode_blocks remaining (serialize_ciphertext encrypted.c :: acc)
in
String.concat " " (encode_blocks message [])