
Stéganographie OCaml
1. Introduction
Ce projet, réalisé pour le module Algorithmique et Complexité, consiste à implémenter un algorithme de stéganographie en OCaml avec chiffrement RSA.
La stéganographie vise à dissimuler une information dans un média anodin. Ici, le message texte est caché dans une image .ppm. Cette méthode permet une communication discrète, le message étant indétectable sans connaître son existence.
Le message inséré est chiffré avec RSA pour garantir sa sécurité. RSA repose sur un couple de clés : la clé privée, conservée par le destinataire pour déchiffrer, et la clé publique utilisée pour chiffrer. Ainsi, n’importe qui peut chiffrer un message, mais seul le détenteur de la clé privée peut le lire.
2. Analyse initiale
Une façon d’insérer discrètement le message est d’utiliser les bits de poids faible de chaque canal couleur de chaque pixel, ce qui permet d’encoder trois bits par pixel. Une image 100×100 contient ainsi 30 000 bits disponibles.
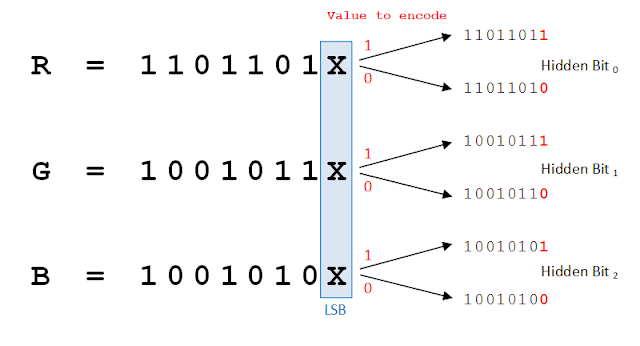
Figure 1.1 : modification du bit de poids faible de chaque pixel.
Plutôt que de parcourir toute l’image et risquer d’ajouter du bruit après la fin du message, nous ajoutons un en-tête de 30 bits (10 pixels) indiquant la longueur du message. On obtient ainsi une complexité O(n) où n est la taille du message.
Le message chiffré est converti en bits avant d’être inséré pour s’adapter au format de l’image.
3. Encodage dans l’image
Une image PPM est un format simple non compressé composé d’un en-tête sur trois lignes :
- type d’image binaire ou ASCII (ici
P6), - largeur et hauteur,
- valeur maximale de couleur (255).
Vient ensuite la liste des valeurs RGB de chaque pixel. La longueur du message est convertie en chaîne binaire sur 30 bits et placée dans les dix premiers pixels.
3.1 Construction du message complet
Le message final regroupe l’en-tête et le message chiffré converti en binaire.
3.2 Écriture dans l’image
Chaque bit du message est inséré séquentiellement dans le bit de poids faible de chaque octet couleur. L’image est chargée en mémoire, modifiée, puis enregistrée sous output.ppm.
3.3 Présentation du code
(* Fonction qui écrase le dernier bit d'un octet avec un bit donné *)
let overwrite_last_bit byte message_bit =
match message_bit with
| '1' -> byte lor 1
| '0' -> byte land 0xFE
| _ -> failwith "Message bit must be '0' or '1'"(* Fonction d'insertion d'un message dans une image PPM *)
let insert_message file_path message =
let ic = open_in_bin file_path in
let oc = open_out_bin "output.ppm" in
(* Lecture et réécriture de l'en-tête *)
let (width, height, max_val) = read_header ic in
Printf.fprintf oc "P6\n%d %d\n%s\n" width height max_val;
let image_size = width * height * 3 in
let buffer = Bytes.create image_size in
really_input ic buffer 0 image_size;
let binary_message = string_to_binary message in
let binary_length = int_to_fixed_length_binary 30 message_length in
let full_message = binary_length ^ binary_message in
let message_index = ref 0 in
for i = 0 to image_size - 1 do
if !message_index < String.length full_message then
let byte = Char.code (Bytes.get buffer i) in
let msg_bit = full_message.[!message_index] in
incr message_index;
Bytes.set buffer i (Char.chr (overwrite_last_bit byte msg_bit));
done;
output_bytes oc buffer;
close_in ic;
close_out oc3.4 Complexité
Complexité de overwrite_last_bit
Cette fonction effectue une simple opération logique sur un octet :
- Temps : O(1)
- Mémoire : O(1)
Complexité de la boucle de traitement
La boucle parcourt chaque octet de l’image pour y insérer les bits du message.
- Temps : O(n) avec n le nombre d’octets de l’image (largeur × hauteur × 3).
- Mémoire : O(1)
4. Chiffrement RSA
RSA est un système cryptographique asymétrique utilisant une clé publique pour chiffrer et une clé privée pour déchiffrer. Sa sécurité repose sur la difficulté de factoriser de grands nombres premiers.
Nous nous sommes appuyés sur le dépôt GitHub RSA-by-OCaml comme base d’implémentation.
4.1 Génération des clés
- Choix des nombres premiers p et q.
- Calcul de .
- Calcul de la fonction indicatrice .
- Choix de l’exposant public e premier avec (souvent 65537).
- Calcul de l’exposant privé d tel que .
4.2 Clés
- Clé publique :
- Clé privée :
4.3 Chiffrement et déchiffrement
- Chiffrement :
- Déchiffrement :
4.4 Sécurité
La sécurité de RSA tient à la difficulté de factoriser en ses facteurs premiers. Un choix judicieux de p, q et e est essentiel pour éviter les attaques.
4.5 Présentation du code
Le code lié à RSA se trouve dans l’annexe.
(* Génération de la clé privée *)
let private_key_gen rc =
let p = prime_gen rc.p_len in
let q = prime_gen rc.q_len in
let phi = Z.mul (Z.sub p Z.one) (Z.sub q Z.one) in
let e = e_gen rc phi in
let d = d_gen e phi in
{ n = Z.mul p q; p; q; e; d }(* Chiffrement d'un message avec la clé publique *)
let plaintext_encrypt pt (pk : public_key) =
let c = Z.powm pt.message pk.e pk.n in
{ c = c; types = pt.types }4.6 Procédure de chiffrement/déchiffrement
Le message est converti en entier, puis l’exponentiation modulaire est utilisée pour chiffrer et déchiffrer selon les formules ci-dessus.
4.7 Utilitaires
- Test de coprimalité (
coprime) - Sérialisation et écriture de fichiers
4.8 Complexité
- Génération des clés : dépend du test de primalité de Miller‑Rabin.
- Chiffrement/Déchiffrement : complexité logarithmique liée à la taille des clés.
5. Résultats
Exemple de sortie du programme :
remybarranco@MacBook-Pro-de-Remy Projet-Algo % cat msg.txt
OCaml is the best language%
remybarranco@MacBook-Pro-de-Remy Projet-Algo % ./encode
Encrypted message inserted into the image
remybarranco@MacBook-Pro-de-Remy Projet-Algo % ./decode
Message length: 1016 bits
Decrypted Message:
OCaml is the best language
remybarranco@MacBook-Pro-de-Remy Projet-Algo %Benchmark pour 100 itérations :
| Taille des données | Opération | Temps (s) |
|---|---|---|
| 10 caractères (512×512) | Encodage | 1.520 |
| Décodage | 0.020 | |
| 100 caractères (512×512) | Encodage | 1.360 |
| Décodage | 0.020 | |
| 10 caractères (5184×3456) | Encodage | 1.920 |
| Décodage | 0.020 | |
| 100 caractères (5184×3456) | Encodage | 1.820 |
| Décodage | 0.020 |
Tableau 1.1 : temps d’encodage et de décodage selon la taille des données
6. Conclusion
Ce rapport présente la stéganographie combinée au chiffrement RSA pour cacher un message dans une image sans en modifier l’apparence. Les figures illustrant l’insertion se trouvent en annexe.
Bien que la théorie RSA ait été vue en cours de cryptographie peu avant la date limite, la mettre en œuvre en OCaml s’est révélée instructif mais ardu à cause de la syntaxe du langage.
7. Références
Annexes
7.1 Code RSA
(* Implémentation RSA (sources/rsa.caml) *)
(* Définition des types de configuration et des clés *)
type rsa_config = { p_len : int; q_len : int; e_len : int }
(* ... *)
(* Vérifie si deux nombres sont premiers entre eux *)
let coprime a b = Z.gcd a b = Z.one
(* Calcule φ(n) pour une liste de nombres premiers *)
let rec prime_phi plist =
match plist with
| [] -> Z.one
| p :: plist' -> Z.mul (Z.sub p Z.one) (prime_phi plist')
(* Exponentiation modulaire *)
let mod_exp a b n = Z.powm a b n
(* Inverse multiplicatif modulaire *)
let mod_minv a n = Z.invert a n
(* Génère un grand entier aléatoire *)
let z_gen (len : int) =
let rec z_gen’ len acc =
if len = 0 then acc
else
z_gen’ (len - 1) (Z.add (Z.mul acc (Z.of_int 10)) (Z.of_int (Random.int 10)))
in
z_gen’ len Z.zero
(* Test de primalité de Miller-Rabin *)
let miller_rabin_test ?(trails = 50) n =
let rec get_factor_q num =
if Z.(mod) num (Z.of_int 2) = Z.zero then
get_factor_q (Z.div num (Z.of_int 2))
else
num
in
if Z.of_int 2 = n then true
else
let q = get_factor_q (Z.sub n Z.one) in
let rec miller_rabin_test’ trails =
if trails = 0 then true
else
let a =
Z.of_int64 (Random.int64 (Z.to_int64 (Z.min n (Z.of_int64 Int64.max_int))))
in
let rec miller_rabin_test’’ expp =
if Z.abs (Z.powm a expp n) = Z.one then miller_rabin_test’ (trails - 1)
else if expp = Z.sub n Z.one then false
else if Z.(mod) (Z.powm a expp n) n = Z.sub n Z.one then
miller_rabin_test’’ (Z.mul expp (Z.of_int 2))
else
false
in
miller_rabin_test’’ q
in
miller_rabin_test’ trails
(* Génère un nombre premier d'une longueur donnée *)
let prime_gen ?(trails = 50) len =
let rec prime_gen’ len =
let p = z_gen len in
if miller_rabin_test ~trails p then p else prime_gen’ len
in
prime_gen’ len
(* Génère un nombre premier avec φ (pour l'exposant e) *)
let e_gen rc phi =
let rec e_gen’ phi =
let e = z_gen rc.e_len in
if coprime e phi then e else e_gen’ phi
in
e_gen’ phi
(* Génère l'exposant privé d via l'inverse modulaire *)
let d_gen e phi = mod_minv e phi
(* Génère une clé privée avec la configuration RSA *)
let private_key_gen rc =
let p = prime_gen rc.p_len in
let q = prime_gen rc.q_len in
let phi = Z.mul (Z.sub p Z.one) (Z.sub q Z.one) in
let e = e_gen rc phi in
let d = d_gen e phi in
{ n = Z.mul p q; p; q; e; d }
(* Génère une clé publique à partir de la clé privée *)
let public_key_gen pk = { n = pk.n; e = pk.e }
(* Encode une chaîne en entier *)
let plaintext_input_string s =
let rec encode acc chars =
match chars with
| [] -> acc
| h :: t -> encode (Z.add (Z.mul acc (Z.of_int 256)) (Z.of_int (Char.code h))) t
in
let encoded = encode Z.zero (List.of_seq (String.to_seq s)) in
{ message = encoded; types = "String" }
(* Chiffre un message avec la clé publique *)
let plaintext_encrypt pt (pk : public_key) =
let c = Z.powm pt.message pk.e pk.n in
{ c = c; types = pt.types }
(* Écrit une chaîne dans un fichier *)
let write_to_file ~filename ~content =
let channel = open_out filename in
output_string channel content;
close_out channel
(* Sérialise une clé privée en chaîne *)
let serialize_private_key pk =
Printf.sprintf "n=%s\np=%s\nq=%s\ne=%s\nd=%s"
(Z.to_string pk.n) (Z.to_string pk.p) (Z.to_string pk.q)
(Z.to_string pk.e) (Z.to_string pk.d)
(* Sérialise un chiffrement en chaîne *)
let serialize_ciphertext c =
Z.to_string c
(* Génère et sauvegarde une clé privée dans un fichier *)
let private_key_gen_and_save rc filename =
let p = prime_gen rc.p_len in
let q = prime_gen rc.q_len in
let phi = Z.mul (Z.sub p Z.one) (Z.sub q Z.one) in
let e = e_gen rc phi in
let d = d_gen e phi in
let pk = { n = Z.mul p q; p; q; e; d } in
let serialized_pk = serialize_private_key pk in
write_to_file ~filename ~content:serialized_pk;
pk
(* Chiffre un message, le découpe en blocs et renvoie le texte chiffré concaténé *)
let encrypt_and_return_message message rc =
let pk = private_key_gen_and_save rc "private_key.txt" in
let public_key = public_key_gen pk in
let block_size = (Z.numbits pk.n) / 8 - 1 in
let rec encode_blocks msg acc =
if msg = "" then List.rev acc
else
let block = String.sub msg 0 (min block_size (String.length msg)) in
let remaining = String.sub msg (min block_size (String.length msg)) (String.length msg - min block_size (String.length msg)) in
let encoded = plaintext_input_string block in
let encrypted = plaintext_encrypt encoded public_key in
encode_blocks remaining (serialize_ciphertext encrypted.c :: acc)
in
String.concat " " (encode_blocks message [])